方差，用来描述数据的离散程度，就是数据的波动性、稳定性。当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小。因此方差越大，数据的波动越大；方差越小，数据的波动就越小。

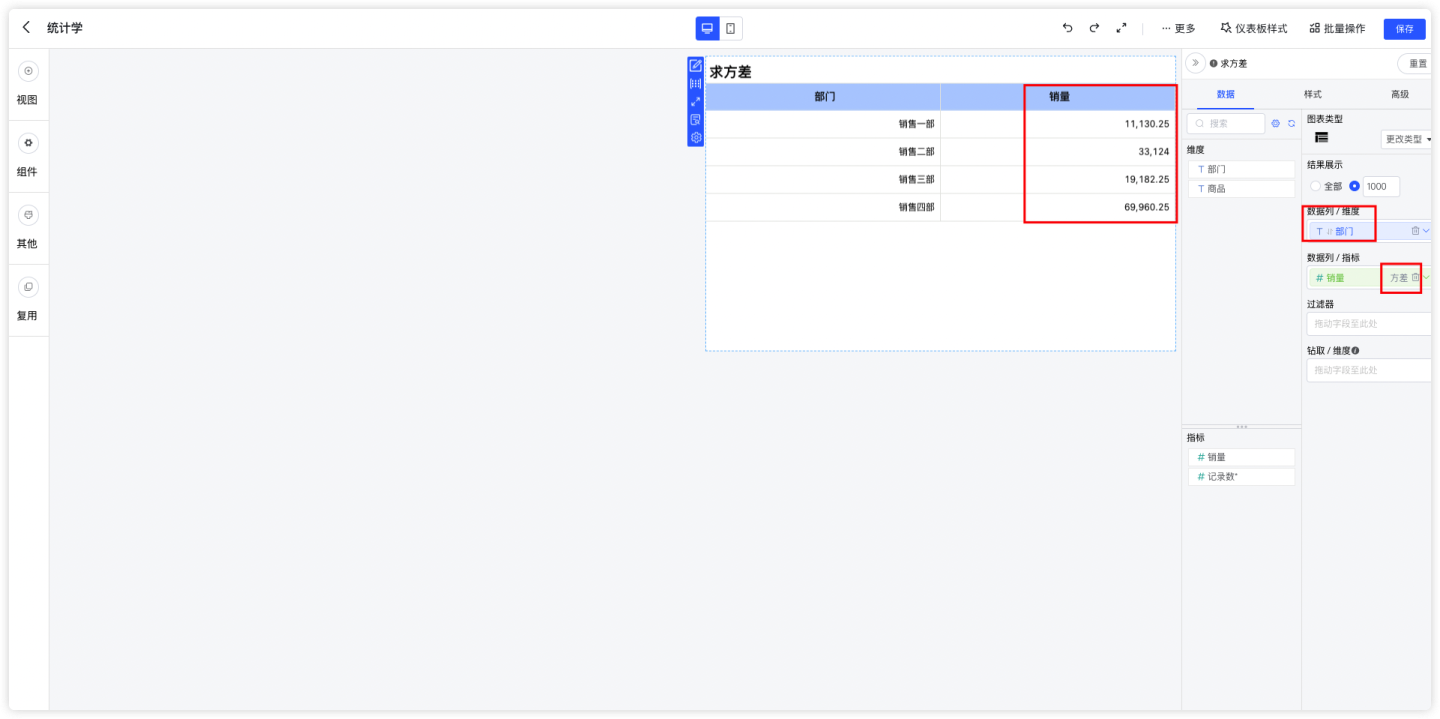
总体方差计算公式：

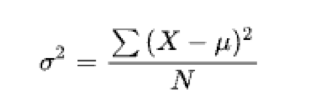
1 在 Excel 中公式

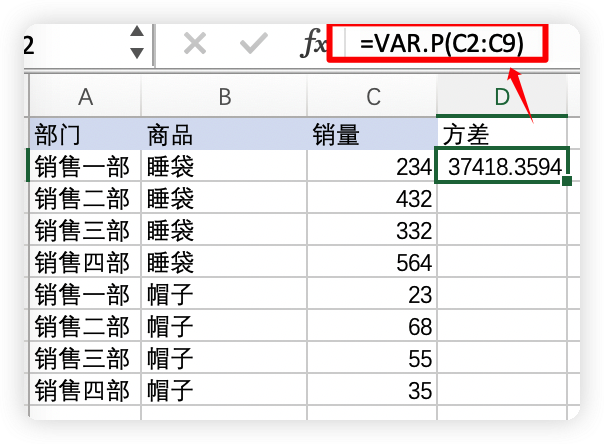
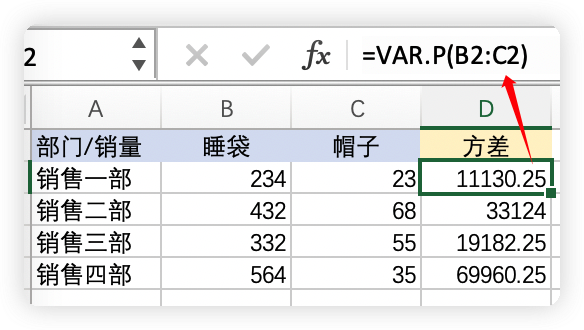
VAR.P 函数计算基于整个样本总体的方差，现用一份运动公司销售数据演示。

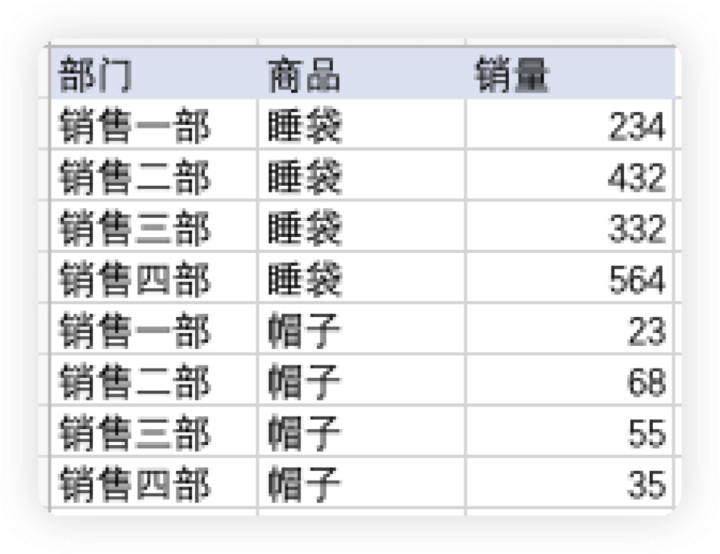
1.1 总销量方差

1.2 各商品销量方差

1.3 各部门销量方差

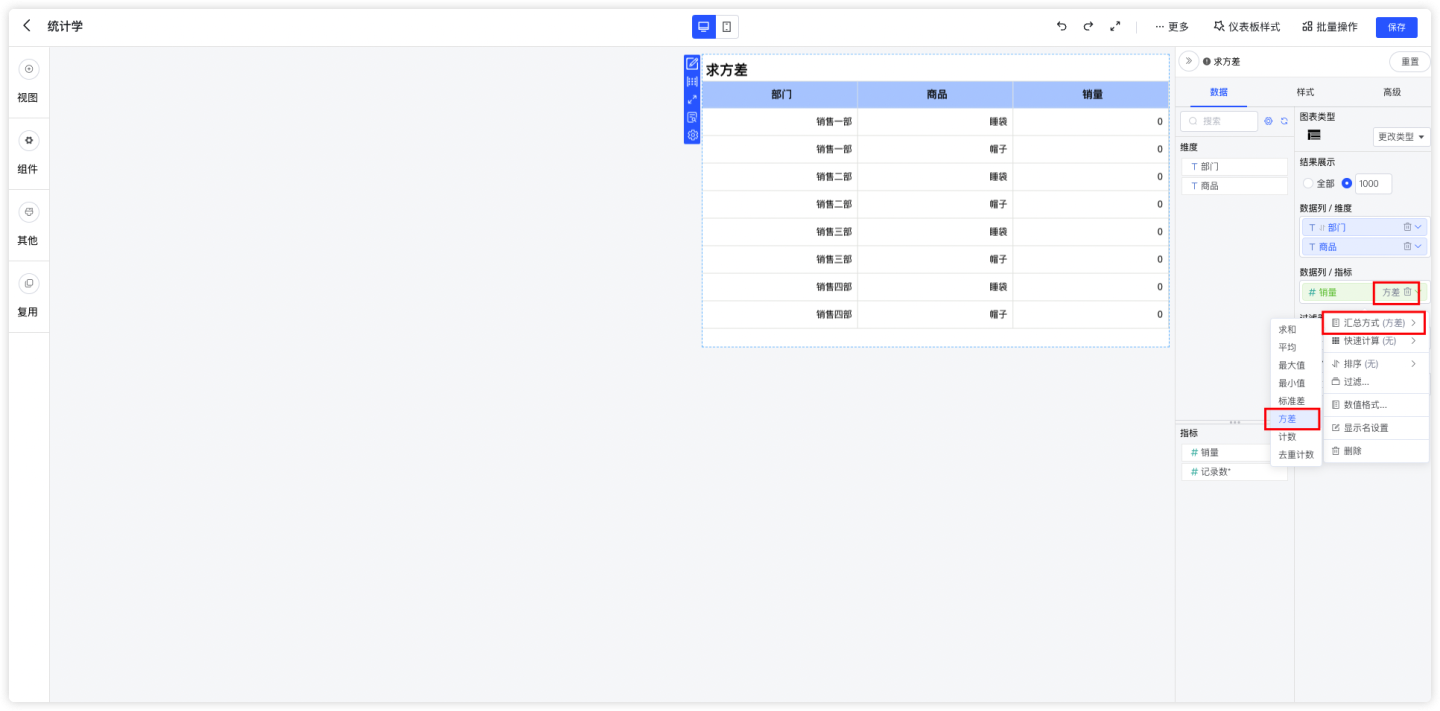
2 在 DataEase 中，无需输入代码及公式

2.1 总销量方差

根据商品和部门两个维度细分后指标为明细数据，所以单指标方差为0 。

将维度都去除，只留销量指标，汇总方式选择方差，得到总销量方差。

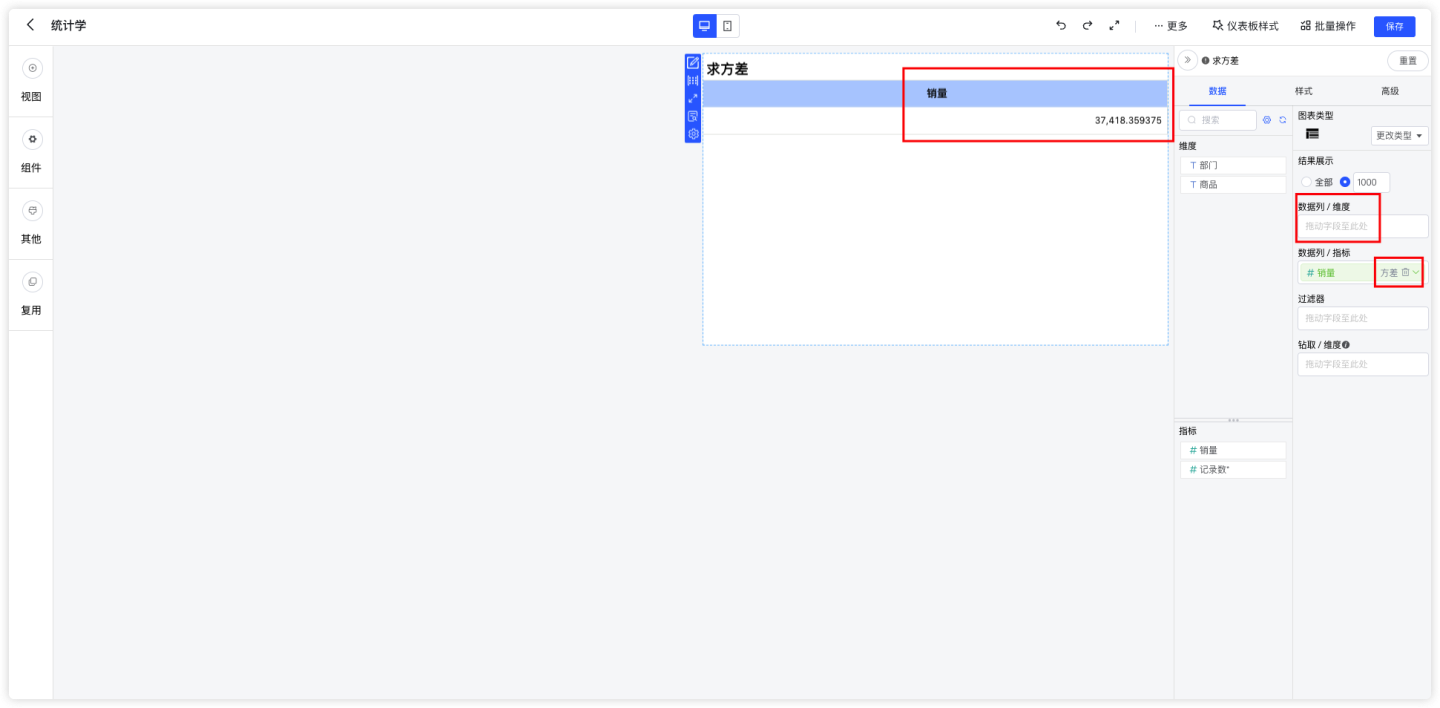
2.2 各商品销量方差

维度去掉部门，只拖入商品，指标销量汇总方式选择方差。

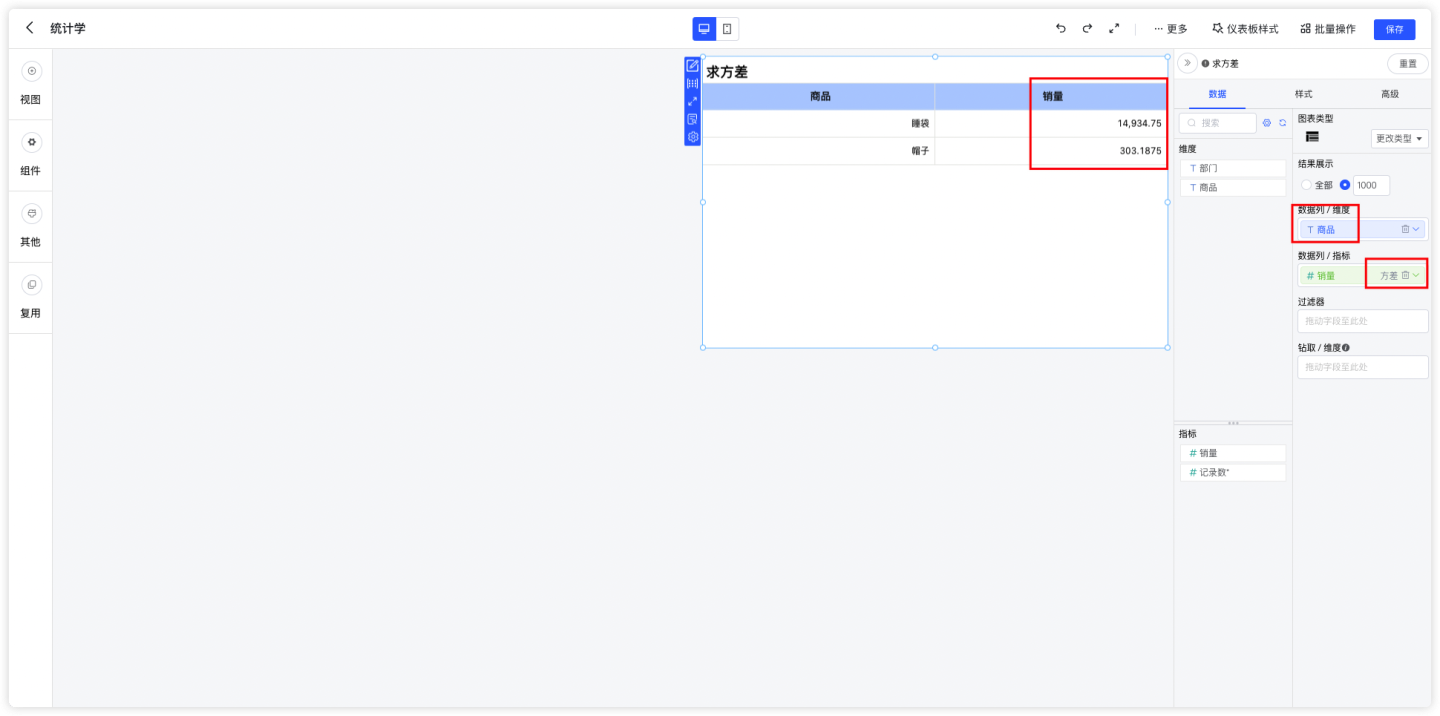
2.3 各部门销量方差

维度去掉商品，拖入部门，指标销量汇总方式选择方差。